金融リテラシー教育の講義資料の作成に没頭していたので、ブログの更新が遅れてしまいました。講義資料の中に『72の法則』の話を載せたので、今回はこの法則について解説したいと思います。
- 『72の法則』は、複利で運用した場合に金融資産が2倍になるまでの年数を計算するときに使うものである
- 2倍になるまでの年数は、72を金利(%)で割って計算することができる
- 『72の法則』で計算した年数は、実際に2倍になる年数より若干長めになる
- 72で割り切れない5%、7%、10%などは『70の法則』で計算してしまって良い
『72の法則』とは
『72の法則』は、複利で運用した場合に、金融資産が2倍になるまでにかかる年数を計算するときに使う法則です。
例えば、金利2%で金融資産を運用する場合、72を2で割った36年で資産が2倍になると計算することができます。
金利r%で複利運用した場合、資産が2倍になるまでの年数nは以下で計算できる。
n = 72 / r
金利を変化させた場合、この法則で2倍になるまでの年数を出してみると、以下の表のようになります。
| 金利(%) | 2倍になるのにかかる年数 |
|---|---|
| 1 | 72 |
| 2 | 36 |
| 3 | 24 |
| 4 | 18 |
| 5 | 14.4 |
| 6 | 12 |
| 7 | 10.3 |
| 8 | 9 |
| 9 | 8 |
| 10 | 7.2 |
金利2%では2倍になるまで36年かかりますが、金利4%で運用できれば18年で金融資産が2倍になります。複利効果は大変大きいことがわかります。
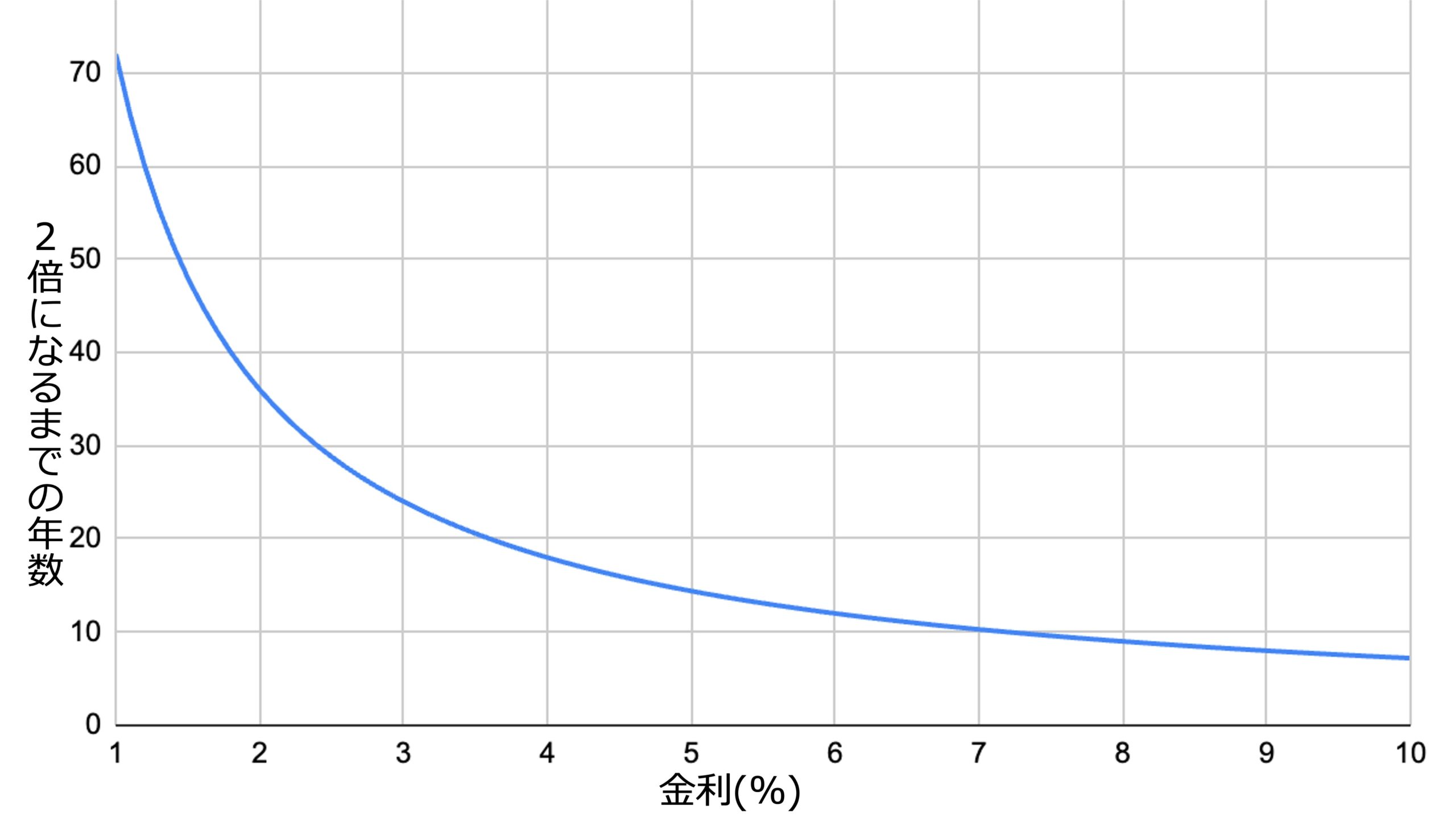
ちなみに、2倍になるまでの年数と金利をグラフにしてみると以下のようになります。
『72の法則』の導出方法
『72の法則』はどのように導かれるのでしょうか。
金利をr%、2倍になるまでの年数をnとした場合、72の法則では以下が成り立つことになります。
n = 72 / r ・・・・・ (1)
ここから先の導出ではちょっと数学の知識が必要ですが、そんなものかと読み進めていただければと思います。
元金をG円、金利をr%、2倍になるまでの年数をnとした場合、以下が成り立ちます。
2 x G = G x (1+r)^n
両辺をGで割ると以下が成り立ちます。
2 = (1+r)^n
これを対数化すると以下が成り立ちます。
ln 2 = n ln(1+r)
右辺の対数の部分を級数展開すると、以下のようになります。
ln 2 = n { r/100 + (r/100)^2/2 + (r/100)^3/3 + (r/100)^4/4 + (r/100)^5/5 + … }
ここで、(r/100)^2/2以下の項は非常に小さいのでゼロに近似してしまうと、以下の式が成り立ちます。
ln 2 ≒ n x r/100
この式をnで解くと、以下になります。
n ≒ 100 x ln 2/r
ln 2は、約0.69なので、上の式は以下のようになります。
n ≒ 100 x ln 2/r
= 100 x 0.69/r
= 69 / r ・・・・・ (2)
72の法則は(1)式だったのですが、実際は(2)式になります。『72の法則』は、実は『69の法則』だったのです。
ではなぜ、『69の法則』ではなく、『72の法則』なのでしょうか。それは72という数字がとても便利な数字だからです。
69の約数が1,3,23,69の4個だけなのに対して、72の約数は1、2、3、4、6、8、9、12、18、24、36、72の12個あります。2%、3%、4%、6%、8%など金利でよく使いそうな数字で割り切れるので、72を使った方が便利ということが、『72の法則』が普及している理由だと考えられます。5%、7%、10%の場合は、72で割り切れないので、その場合は『70の法則』にして計算を簡略化できることもわかります。
『69の法則』を『72の法則』で代用した場合、『69の法則』で計算した年数より若干長めの答えになるということも覚えておくと良いでしょう。
まとめ
今回は、『72の法則』について解説しました。実際は『69の法則』なので、5%、7%、10%など72で割り切れない金利の場合は、割り切れる70を使って『70の法則』で計算してもらえればと思います。
最後までお読みいただき、ありがとうございます。
1級ファイナンシャルプランニング技能士
CFP®️認定者
1級DCプランナー